Option Pricing Using The Binomial Model

Binomial models (and there are several) are arguably the simplest techniques used for option pricing. The mathematics behind the models is relatively easy to understand and (at least in their basic form) they are not difficult to implement.

This tutorial discusses the general mathematical concepts behind the binomial model with particular attention paid to the original binomial model formulation by Cox, Ross and Rubinstein (CRR). An example of implementing the CRR model in MATLAB can be found in a this tutorial.

However, there are many other versions of the binomial model. Several of them, including a discussion of their underlying mathematics and an example of their implementation in MATLAB, are presented in a companion option pricing tutorial.

Each of the approaches has its advantages and disadvantages for pricing different types of options. However, they all involve a similar three step process.

1. Calculate potential future prices of the underlying asset(s) at expiry (and possibly at intermediate points in time too).
2. Calculate the payoff of the option at expiry for each of the potential underlying prices.
3. Discount the payoffs back to today to determine the option price today.

Each of those steps is discussed in the following sections.

Calculating a Tree for the Underlying Asset Price

The first step in pricing options using a binomial model is to create a lattice, or tree, of potential future prices of the underlying asset(s). This section discusses how that is achieved.

The One Step Binomial Model

A one-step binomial model is shown in Figure 1. The notation used is,

• S₀: The stock price today.
• p: The probability of a price rise.
• u: The factor by which the price rises (assuming it rises).
• d: The factor by which the price falls (assuming it falls).

Note that the model assumes that the price of the equity underlying the option follows a random walk.

Figure 1: One Step Binomial Model

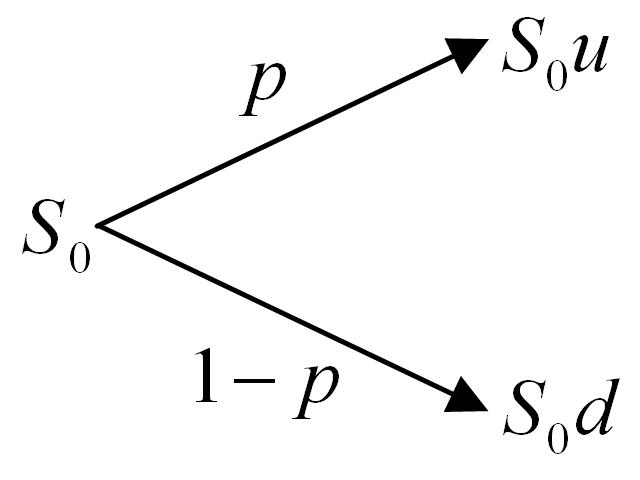
The essence of the model is this: assume the price of an asset today is S₀ and that over a small time interval Δt it may move to one of only two potential future values S₀u or S₀d. The underlying price is assumed to follow a random walk and a probablity p is assigned to the likelihood that the price will rise. Hence the probability of a fall in the stock price is 1-p.

Conceptually any values for the three parameters, p, u and d may be used. (Subject to 0 < p < 1 and S₀d > 0.) However some values are more optimal than others. So the question is how can the best values be calculated?

There is no simple answer to that question. In fact there are many different approaches to calculating values for p, u and d. These include methods developed by,

• Cox-Ross-Rubinstein: This is the method most people think of when discussing the binomial model, and the one discussed in this tutorial.
• Jarrow-Rudd: This is commonly called the equal-probability model.
• Tian: This is commonly called the moment matching model.
• Jarrow-Rudd Risk Neutral: This is a modification of the original Judd-Yarrow model that incorporates a risk-neutral probablity rather than an equal probability.
• Cox-Ross-Rubinstein With Drift: This is a modification of the original Cox-Ross-Runinstein model that incorporates a drift term that effects the symmetry of the resultant price lattice.
• Leisen-Reimer: This uses a completely different approach to all the other methods, relying on approximating the normal distrbution used in the Black-Scholes model.

Of the above approaches the Cox-Ross-Rubinstein method is perhaps the best known, with the Jarrow-Rudd method close behind. The remaining methods have been developed to address perceived (and perhaps real) deficiencies in those two methods.

A Risk-Neutral World

Three equations are required to be able to uniquely specify values for the three parameters of the binomial model. Two of these equations arise from the expectation that over a small period of time the binomial model should behave in the same way as an asset in a risk neutral world.

This leads to the equation

Equation 1: Matching Return
which ensures that over the small period of time Δt the expected return of the binomial model matches the expected return in a risk-neutral world, and the equation, Equation 2: Matching Variance
which ensures that the variance matches.

Cox-Ross-Rubinstein

Cox, Ross and Rubinstein proposed the third equation

Equation 3: Third Equation for the Cox-Ross-Rubinstein Binomial Model

Rearranging the above three equations to solve for parameters p, u and d leads to,

Equation 4: Equations for the Cox-Ross-Rubinstein Binomial Model

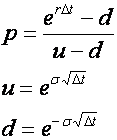
The unique solution for parameters p, u and d given in Equation 4 ensures that over a short period of time the binomial model matches the mean and variance of an asset in a risk free world, and as will be seen shortly, ensures that for a multi-step model the price of the underlying asset is symmetric around the starting price S₀.

The Multi-Step Model

Before considering the more general case of a many-step model, consider the two-step model shown in Figure 2

Figure 2: A Two-Step Binomial Model

As with the one-step model of Figure 1, over the first period of time in the two-step model the asset price may move either up to S_u or down to S_d. Over the second period, if the price moved up to S_u in the first period then the price may move to either S_uu or S_ud. However if the price moved down in the first period to S_d then in the second period it may move to either S_du or S_dd.

If S_ud=S_du then the price tree is said to be recombining. However if they are not equal then the price tree is said to be non-recombining (or bushy).

Since there are typically tens if not hundred or thousands of time steps taken when pricing an option the amount of data (and hence computer memory, and computation time) required to calculate a non-bushy tree is typically prohibitively and hence they are rarely used.

The third equation of the CRR model ensures that it generates a recombining tree that is centred around the original stock price S₀. Taking multiple time steps leads to the tree shown in Figure 3.

Figure 3: A Multi-Step Binomial Model

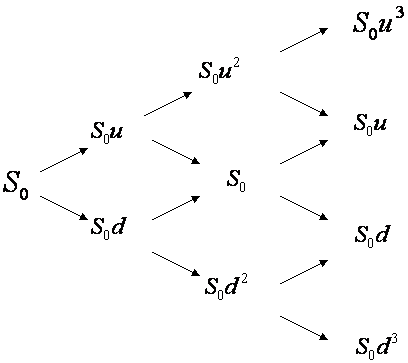
In general the time period between today and expiry of the option is sliced into many small time periods. A tree of potential future asset prices is then calculated. Each point in the tree is refered to as a node. The tree contains potential future asset prices for each time period from today through to expiry.

Calculating the Payoffs at Expiry

The second step in pricing options using a binomial model is to calculate the payoffs at each node corresponding to the time of expiry. This corresponds to all of the nodes at the right hand edge of the price tree.

In general the payoff may depend on many different factors. As an example, the payoffs of simple put and call options will use the standard formulae

Type Payoff Put VN = max(X-SN,0) Call VN = max(SN-X,0)

where

• N designates a node at expiry.
• V_N is the option value.
• X is the strike.
• S_N is the price of the underlying asset.

Discounting the Payoffs

The third step in pricing options using a binomial model is to discount the payoffs of the option at expiry nodes back to today. This is achieved by a process called backwards induction, and involves stepping backwards through time calculating the option value at each node of the lattice in a sequential manner.

This is achieved using the appropriate following formulae

Type Backwards Induction Formula European Put or Call Vn = e-rΔt(pVu+(1-p)Vd) American Put Vn = max(X-Sn,e-rΔt(pVu+(1-p)Vd)) American Call Vn = max(Sn-X,e-rΔt(pVu+(1-p)Vd))

where

• n designates a node prior to expiry.
• V_n is the option value.
• X is the strike.
• S_n is the price of the underlying asset.
• p is the probability of an upwards price movement.
• V_u is the option value from node upper node at n+1.
• V_u is the option value from the lower node at n+1.
• r is the risk-free interest rate.
• Δt is the step size between time slices of the model.

It is critical to notice that with backwards inducton the counter n starts at N (i.e. expiry) and decreases down to 0 (i.e. today).

The Option's Value

Following the three step procedure described above the value of the option V₀ may be calculated. A MATLAB implementation of the CRR algorithm presented here can be found in this tutorial.

A companion option pricing tutorial discusses the mathematics behind several alternative binomial models.

Back To Top | Option Pricing