Monte-Carlo Option Pricing - Variance Reduction
A significant drawback of Monte-Carlo simulation methods for option pricing is that typically a very large number of simulated future asset prices are required to obtain an accurate solution. This tutorial describes several techniques that are commonly applied to reduce the number of simulated paths that need to be generated to achieve a given level of confidence in the calculated option price.
The general mathematical concepts underlying Monte-Carlo simulation are discussed in the Monte Carlo Methods tutorial. Examples of implementing the methods discussed in this tutorial in MATLAB can be found on the Software Tutorials page.
In this tutorial the following so called variance reduction techniques are considered,
Confidence Bounds
When pricing options using Monte-Carlo methods a confidence bound can often be placed around the calculated option price. This bound is typically a function of the number of simulation paths generated (N), and the mean (μ) and variance (σ) of the payoffs for all of the generated paths.
For example, for options where the underlying assets is assumed to follow a log-normal distribution (as per the stock price evolution equation for equities given in the Monte Carlo Methods tutorial) then the following confidence bound can be placed on the resulting option price
![]()
Hence the confidence interval can be reduced (and a more accurate price obtained) by either increasing the number of simulated paths N, or by reducing the variance of the payoffs σ.
The techniques discussed in this option pricing tutorial aim (generally speaking) to obtain a better price by reducing σ and hence are refered to as variance reduction techniques. Although they can (and are) often applied together, in this tutorial they are considered individually.
Antithetic Variates
Antithetic variates is based on the premise that under certain conditions using N/2 pairs of sample paths that are negatively correlated rather than N individually generated paths leads to a tighter confidence interval.
To see this consider two randomly generated paths
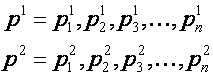
Then the path pi where
![]()
is formed from the average of p1 and p2 will also be a valid path.
If pN is the average of N such paths
then its variance is given by
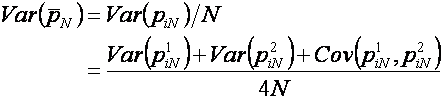
which is minimized if the sample path pair is perfectly negatively correlated.
Hence the result that the variance (and hence the bound on the option price) will be smallest if N/2 pairs of sample paths that are negatively correlated, rather than N individually generated paths, are used.
In practise the pairs are generated by using ε (a sample from a random distribution) to generate one path and -ε to generate another path. This use of complimentary random numbers turns out to only work (i.e generate a better option price) if the option's payoff function is monotonic with the underlying asset price. That is, it never decreases (as with a vanilla Call) or it never increases (as with a vanilla Put).
An example of MATLAB code for generating simulation paths using antithetic variates and using them to price an Asian option can be found in the Using Antithetic Variates in MATLAB tutorial. Other MATLAB based Monte-Carlo tutorials are linked off the Software Tutorials page.
Control Variates
The Control Variates method is based on the premise that if the pricing algorithm misprises an option that has a known price, then it will misprice an option that doesn't have a known value by a similar amount. In its basic form this can be expressed mathematically as,
PX = PX + (PY - PY)
where
- PX is an estimate of the price of the option on X (obtained using Monte-Carlo methods).
- PX is a better estimate of the price of the option on X (and the one that will be used).
- PY is a known price of a similar option on Y
- PY is an estimated price of the similar option on Y (obtained using Monte-Carlo methods).
Best results are typically obtained when the asset Y is similar (in some sense) to asset X and the types of options being priced are also similar.
More generally the following mathematical formulation may be used,
PX = PX + k(PY - PY)
where k is a parameter that needs to be calculated.
Note that since a goal is to minimize the variance of the price, and the variance is given by
Var(PX) = Var(PX) + k2Var(PY) + 2kCov(PX,PY)
then a natural choice for k (obtained by setting the derivative of the above equation with respect to k equal to zero) is
kopt = Cov(PX,PY)/ Var(PY).
Unfortunately the data required to calculate kopt is typically not known a-priori and must be calculated by performing simulations prior to the pricing simulation. The time taken in performing this additional simulation may negate any speed advantage in using control variates.
An example of MATLAB code for generating simulation paths using control variates and using them to price an Asian option can be found in the Using Control Variates in MATLAB tutorial. Other MATLAB based Monte-Carlo tutorials are linked off the Software Tutorials page.
Importance Sampling
If an option is a long way out of the money (or more generally if rare events that may occur during the life of an option need to be considered) then a large number of the simulated paths may end out of the money too. Importance Sampling is a method that attempts to only generate sample paths that have a high probability of being significant to the caculated price, i.e. in the money. Paths that lead to a zero payoff are less likely to be generated.
Importance sampling is achieved by distorting the probability distribution from which random samples are taken. Unfortunately, in many instance determining an appropriate new/distorted distribution can be a non-trivial process.
Quasi-Random Sequences
Underlying the use of Monte-Carlo simulation is the requirement to sample from a suitable random distribution. However, computers do not generate truly random numbers - rather they generate pseudo-random numbers. These are numbers generated in a purely deterministic way, which, when enough of them are considered together, satisfy standard statistical tests which makes them look like they are random.
Pseudo-random sequences are used by most numerical analysis software packages to generate random numbers. For instance MATLAB's standard rand and randn functions (as well as the probability sampling functions in the Statistics Toolbox), Excel's Rand() function, and R's runif function (as well as other probability sampling functions) all sample from random distributions using pseudo-random sequence generators.
The question then arises whether there are different types of deterministic sequences that exhibit random behaviour. The answer is yes. In addition to pseudo-random sequences there are a class of sequences called low discrepancy or quasi-random sequences. There are several different algorithms for generating quasi-random sequences, including the Sobol and Halton methods (named after the people who initially proposed them).
Quasi-random numbers may be used in Monte-Carlo simulation in the same way as pseudo-random numbers. In some instances the confidence interval for the option price (given in Equation 1) becomes a function of N rather than √ N , and hence gives a more accurate option price for a fewer number of simulation paths.
Halton's Sequence
Halton's sequence is one of several available low discrepancy sequences.
If n is an integer in base 10 (i.e. decimal notation) then it may be written in base
b as
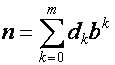
Then the n th number in the Halton sequence of base b is given by
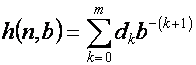
As an example, consider the case of base b = 2. The following table shows how to calculate the first 7 numbers in the Halton sequence of base 2,
|
Table 1: First 7 Elements of Halton's Sequence using base 2.
Notice that the Halton sequence is essentially filling in the largest gap in the range 0 to 1 that doesn't already contain a number in the sequence. Also note that all numbers in the resulting sequence lie between 0 and 1 (which is similar to a uniform distribution). Since samples similar to a normal distribution are required for option pricing the generated numbers must be further manipulated before being useful. One method for converting these uniform numbers to normal numbers is called the Box-Muller transform, which is discussed in the next section.
Note that a different Halton sequence will be generated depending on the base b that is used. For option pricing a sequence with a prime number as its base is usually prefered.
The Box-Muller Transform
There are several different approaches available for transforming a series of numbers that might appear to be derived from a uniform distribution to a series that appears to be derived from a normal distribution. The simplest (although the least numerically stable and hence rarely used) approach is an algorithm called the Box-Muller transformation.
Assume X and Y are two independent random samples on the interval (0,1] then
P = R cos(Θ)
Q = R sin(Θ)
where
R = -2 ln(X)
Θ = 2 π Y
may be treated as samples from a normal distribution. Hence a Halton sequence (or any other low discrepancy sequence) in conjunction with the Box-Muller transformation may be used to generate normal random samples for use with the Monte-Carlo option pricing method.
An example of MATLAB code for generating simulation paths using Halton's quasi-random sequence and using them to price an Asian option can be found in the Halton's Quasi-Random Sequence in MATLAB tutorial. Other MATLAB based Monte-Carlo tutorials are linked off the Software Tutorials page.