Simulink S-Functions - Replicating the Continuous Time Integrator
This example presents both m-code and c-mex versions of a Simulink S-Function that mimics the basic behaviour of a continuous time integrator. Although there would be no need to do this in practise, it is a useful introduction to the Simulink S-Function API and how to use the appropriate S-Function macros.
The example is split into the three sections,
- Dynamic Equations for an Integrator.
- M-Code S-Function Implementation.
- C-Mex S-Function Implementation.
Other tutorials that present examples of S-Functions are available on the Writing Simulink S-Functions page and tutorials discussing Simulink and its applications for model based design are available on the Software Tutorials page.
Dynamic Equations for an Integrator
A single continuous time integrator is modeled using one of the simplest sets of dynamic equations. The equations are,
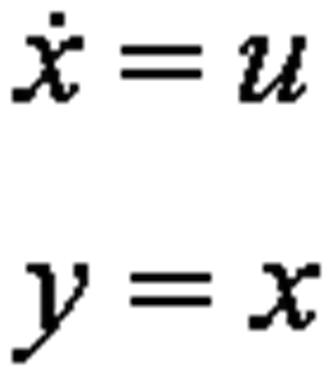
Given the equations in Equation 1 the S-Functions will each have three core methods: the first to initialize the S-Function (c-mex S-Functions have 3 initialization methods); the second to update the state derivative equation; and the third to update the block output.
A simple model that will act as a test harness for the S-Functions developed here is shown in Figure 1. It comprises a Sine Wave block feeding into an integrator, the m-code S-Function and the c-mex S-Function. Note that when the model is run the display on the Scope shows only one line, i.e. all three blocks produce the same result -- as should be expected.
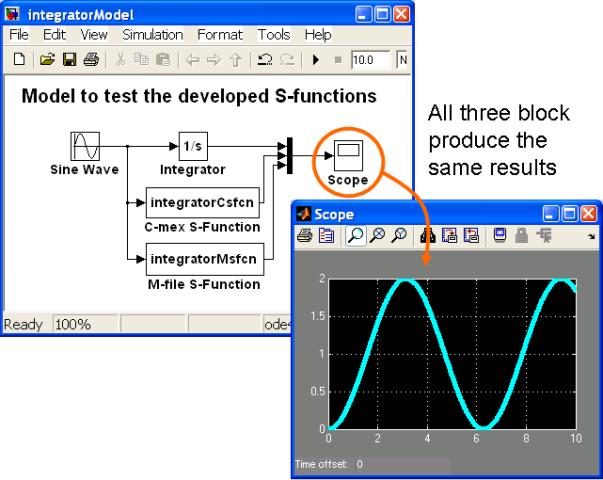
A zip file containing the test harness model and the code for both of the S-Functions may be downloaded here.
M-Code S-Function Implementation
This section contains an m-code implementation of the equations for an integerator (as given in Equation 1).
The m-code S-Function contains four methods: setup; InitializeConditions; Outputs; and Derivatives. The setup method is called by Simulink when a model containing the S-Function is initialized. It tells Simulink about the system being modeled, including how many parameters the user must specify, how many inputs and outputs to expect, whether there are continuous and discrete states and if so how many, the sample rate at which the system needs to be updated, and whether the system has direct feedthrough (of the input to the output). All that information is used by Simulink to determine how the block is to simulated.
The InitializeConditions method is used to initialize any (continuous and discrete) states. In this case the initial state value is specified by the user and the parameter entered by the user is read and used to initialize the state.
The Output method is used to implement the block’s output equation(s). While the Derivatives method implements its state update equation(s).
function integratorMsfcn(block) % Example Level-2 M file S-Function. % This S-function implements a continuous time integrator. % For more details about S-functions, see simulink\blocks\msfuntmpl.m % % Author: Phil Goddard (phil@goddardconsulting.ca) setup(block); %endfunction function setup(block) % Register number of dialog parameters block.NumDialogPrms = 1; % Register number of input and output ports block.NumInputPorts = 1; block.NumOutputPorts = 1; % Setup functional port properties to dynamically be inherited. block.SetPreCompInpPortInfoToDynamic; block.SetPreCompOutPortInfoToDynamic; block.InputPort(1).Dimensions = 1; block.InputPort(1).DirectFeedthrough = false; block.OutputPort(1).Dimensions = 1; % Set block sample time to continuous block.SampleTimes = [0 0]; % Setup Dwork block.NumContStates = 1; % Set the block simStateCompliance to default (i.e., same as a built-in block) block.SimStateCompliance = 'DefaultSimState'; % Register block methods block.RegBlockMethod('InitializeConditions', @InitConditions); block.RegBlockMethod('Outputs', @Output); block.RegBlockMethod('Derivatives', @Derivative); %endfunction function InitConditions(block) % Initialize Dwork block.ContStates.Data = block.DialogPrm(1).Data; %endfunction function Output(block) % y = xdot block.OutputPort(1).Data = block.ContStates.Data; %endfunction function Derivative(block) % xdot = u block.Derivatives.Data = block.InputPort(1).Data; %endfunction
C-Mex S-Function Implementation
This section contains a C-mex implementation of the equations for an integerator (as given in Equation 1).
The c-mex S-Function contains seven methods: mdlInitializeSizes; mdlInitializeSampleTimes; mdlInitializeConditions; mdlCheckParameters; mdlOutputs; mdlDerivatives; and mdlTerminate.
The methods mdlInitializeSizes, mdlInitializeSampleTimes, mdlOutputs, and mdlTerminate are required and must be defined in a c-mex S-Function. There are also several pieces of header information (near the top of the file) and footer information (at the end of the file) that are required.
However mdlInitializeConditions is only required when the system has states (either continuous or discrete), mdlCheckParameters is only required if there is a desire to error check any user specified parameters, while mdlDerivatives is only required if there are continuous states. (These are only several of many different optional methods that are available for use within a c-mex S-Function).
/* File : integratorCsfcn.c * Abstract: * * Example C-mex S-function. * This S-function implements a continuous time integrator. * For more details about S-functions, see simulink/src/sfuntmpl_doc.c. * * Author: Phil Goddard (phil@goddardconsulting.ca) */ #define S_FUNCTION_NAME integratorCsfcn #define S_FUNCTION_LEVEL 2 #include "simstruc.h" /*====================* * S-function methods * *====================*/ /* Function: mdlInitializeSizes ========================================== * Abstract: * The sizes information is used by Simulink to determine the S-function * block's characteristics (number of inputs, outputs, states, etc.). */ static void mdlInitializeSizes(SimStruct *S) { ssSetNumSFcnParams(S, 1); /* Number of expected parameters */ if (ssGetNumSFcnParams(S) != ssGetSFcnParamsCount(S)) { return; /* Parameter mismatch will be reported by Simulink */ } ssSetNumContStates(S, 1); ssSetNumDiscStates(S, 0); if (!ssSetNumInputPorts(S, 1)) return; ssSetInputPortWidth(S, 0, 1); ssSetInputPortDirectFeedThrough(S, 0, 0); if (!ssSetNumOutputPorts(S, 1)) return; ssSetOutputPortWidth(S, 0, 1); ssSetNumSampleTimes(S, 1); ssSetNumRWork(S, 0); ssSetNumIWork(S, 0); ssSetNumPWork(S, 0); ssSetNumModes(S, 0); ssSetNumNonsampledZCs(S, 0); ssSetSimStateCompliance(S, USE_DEFAULT_SIM_STATE); } /* Function: mdlInitializeSampleTimes ==================================== * Abstract: * Specifiy that we have a continuous sample time. */ static void mdlInitializeSampleTimes(SimStruct *S) { ssSetSampleTime(S, 0, CONTINUOUS_SAMPLE_TIME); ssSetOffsetTime(S, 0, 0.0); } #define MDL_INITIALIZE_CONDITIONS /* Function: mdlInitializeConditions =================================== * Abstract: * Initialize both continuous states to zero. */ static void mdlInitializeConditions(SimStruct *S) { real_T *pr = mxGetPr(ssGetSFcnParam(S,0)); real_T *x0 = ssGetContStates(S); *x0 = *pr; /* pr[0]; */ } #define MDL_CHECK_PARAMETERS #if defined(MDL_CHECK_PARAMETERS) && defined(MATLAB_MEX_FILE) /* Function: mdlCheckParameters ======================================== * Abstract: * The parameter must be double scalar */ static void mdlCheckParameters(SimStruct *S) { int_T i; for (i = 0; i < ssGetNumSFcnParams(S); i++) { real_T *pr; int_T el; int_T nEls; if (mxIsEmpty(ssGetSFcnParam(S,i)) || !mxIsDouble(ssGetSFcnParam(S,i)) ) { ssSetErrorStatus(S,"The parameter must be a finite scalar double"); return; } pr = mxGetPr(ssGetSFcnParam(S,i)); nEls = mxGetNumberOfElements(ssGetSFcnParam(S,i)); if (nEls != 1){ ssSetErrorStatus(S,"The paramater must be a scalar double"); return; } /* Since there is only one element the following does not */ /* need to be a loop */ for (el = 0; el < nEls; el++) { if (!mxIsFinite(pr[el]) || !mxIsNaN(pr[el])) { ssSetErrorStatus(S,"The parameter must be a finite scalar double"); return; } } } } #endif /* MDL_CHECK_PARAMETERS */ /* Function: mdlOutputs ================================================== * Abstract: * y = x; */ static void mdlOutputs(SimStruct *S, int_T tid) { real_T *y = ssGetOutputPortRealSignal(S,0); real_T *x = ssGetContStates(S); /* y[0] = x[0] */ *y = *x; } #define MDL_DERIVATIVES /* Function: mdlDerivatives ============================================ * This is an option method only needed if there are continuous deriv's. * Abstract: * xdot = u */ static void mdlDerivatives(SimStruct *S) { real_T *dx = ssGetdX(S); InputRealPtrsType uPtrs = ssGetInputPortRealSignalPtrs(S,0); /* xdot = u */ dx[0] = *uPtrs[0]; } /* Function: mdlTerminate ================================================ * Abstract: * No termination needed, but method is required. */ static void mdlTerminate(SimStruct *S) { } #ifdef MATLAB_MEX_FILE /* Is this file being compiled as a MEX-file? */ #include "simulink.c" /* MEX-file interface mechanism */ #else #include "cg_sfun.h" /* Code generation registration function */ #endif
This example has presented code for both an m-code and c-mex S-function that replicates the basic functionality of a continuous time integrator.
Other tutorials that present examples of S-Functions are available on the Writing Simulink S-Functions page and tutorials discussing Simulink and its applications for model based design are available on the Software Tutorials page.