Simulink S-Functions - A Square Wave With Jitter
This example presents a Simulink m-code S-Function that implements a square wave signal generator where the time at which the signal rises and falls may be randomly advanced or delayed about a nominal period. This effecively models a square wave pulse with (random) jitter.
The example is split into two sections,
Other tutorials that present examples of S-Functions are available on the Writing Simulink S-Functions page and tutorials discussing Simulink and its applications for model based design are available on the Software Tutorials page.
Description and Test Model
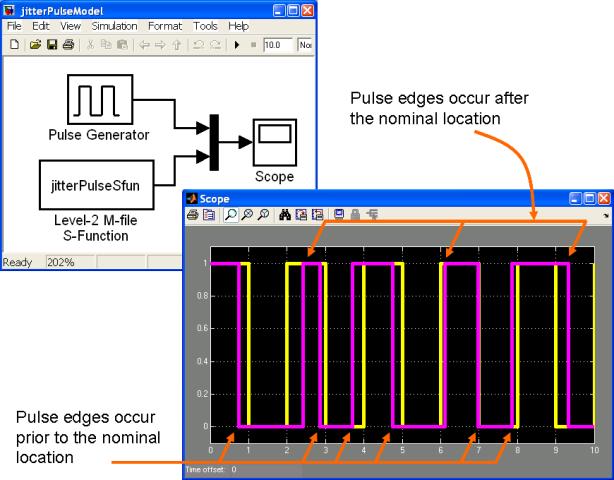
A simple model that will act as a test harness for this model is shown in Figure 1. A zip file containing the test harness model and the S-Function code may be downloaded here.
The output of the S-Function is nominally a square wave with a user specified sample period. However, both the rising and falling edges of the square wave can be made to occur at a random time either prior to, or after, the nominal period.
In Figure 1 the output of the S-Function is superimposed over a standard square wave with the same nominal period. The (random) jitter period has been set to its maximum, which is 25% of the nominal sample period.
M-Code S-Function Implementation
This section gives a description of the m-code contained in the S-Function. Comments in the code are intended to describe the operation of each of the parts of the S-Function, however additional comments have been interspersed between sections of the code.
The first function in the code is called the primary function, and contains only general comments and a call the the setup method of the S-Function.
function jitterPulseSfun(block) %jitterPulse % % This is a level-2 m-code S-Function that acts as a pulse generator with % jitter. % % The user specifies % 1) a nominal period for the pulse (i.e. the nominal time between rising % pulses) % 2) the time that the pulse may be (randomly) delayed or advanced at each % time step. The block assumes a nominal 50% duty cycle, hence this must % be less than 1/4 of the nominal period. % 3) whether the pulse is initially high or low. % % Author: Phil Goddard (phil@goddardconsulting.ca) %% %% The setup method is used to setup the basic attributes of the %% S-function such as ports, parameters, etc. Do not add any other %% calls to the main body of the function. %% setup(block); %endfunction
The setup method is used to initialize the S-Function. It must tell Simulink everything about the block, including the number of inputs, outputs, continuous states and discrete states. Properties of the ports (i.e. inputs and outputs) must be defined; the number of expected parameters and their properties specified; and the sample time/rate specified.
This particular block, since it is a source block, has no inputs and one output. Three parameters must be specied and they are defined to be Nontunable, which implies they cannot be changed while a simulation is being performed.
Of particular importance for this specific block is that it has a variable sample rate. This implies that it can only be used with a Variable Step Solver. This should be expected since the rising and falling edges of the pulses by definition do not fall at predeterminable sample times.
Finally all other block methods must be registered. This particular S-Function has five methods.
%% Function: setup =================================================== %% Abstract: %% Set up the S-function block's basic characteristics such as: %% - Input ports %% - Output ports %% - Dialog parameters %% - Options %% %% Required : Yes %% C-Mex counterpart: mdlInitializeSizes %% function setup(block) % Register number of ports block.NumInputPorts = 0; block.NumOutputPorts = 1; % Setup port properties to be inherited or dynamic block.SetPreCompOutPortInfoToDynamic; % Override output port properties block.OutputPort(1).DatatypeID = 0; % double block.OutputPort(1).Complexity = 'Real'; block.OutputPort(1).SamplingMode = 0; % no frames % Register parameters block.NumDialogPrms = 3; block.DialogPrmsTunable = {'Nontunable','Nontunable','Nontunable'}; % Register sample times % [0 offset] : Continuous sample time % [positive_num offset] : Discrete sample time % % [-1, 0] : Inherited sample time % [-2, 0] : Variable sample time block.SampleTimes = [-2 0]; %% ----------------------------------------------------------------- %% Options %% ----------------------------------------------------------------- % Specify if Accelerator should use TLC or call back into % M-file block.SetAccelRunOnTLC(false); %% ----------------------------------------------------------------- %% The M-file S-function uses an internal registry for all %% block methods. You should register all relevant methods %% (optional and required) as illustrated below. You may choose %% any suitable name for the methods and implement these methods %% as local functions within the same file. %% ----------------------------------------------------------------- block.RegBlockMethod('CheckParameters', @CheckPrms); block.RegBlockMethod('PostPropagationSetup', @DoPostPropSetup); block.RegBlockMethod('Start', @Start); block.RegBlockMethod('Outputs', @Outputs); block.RegBlockMethod('Update', @Update);
The CheckParameters method is called to validate the user specified parameters at the beginning of the simulation. In this case three parameters must be specified and they must have certain properties, otherwise an error is thrown.
%% ------------------------------------------------------------------- %% Local Function to Error Check the Block Parameters %% ------------------------------------------------------------------- function CheckPrms(block) % The period must positive period = block.DialogPrm(1).Data; if ~strcmp(class(period), 'double') || (period <=0) DAStudio.error('Simulink:block:invalidParameter'); end % The advance/delay must be < 25% of the period window = block.DialogPrm(2).Data; if ~strcmp(class(window), 'double') || ... (period <=0) || ... (window >= period/4) DAStudio.error('Simulink:block:invalidParameter'); end % The initial value must be 0 or 1 initVal = block.DialogPrm(3).Data; if ~strcmp(class(initVal), 'double') || ... ~(abs(initVal-0)<2*eps || abs(initVal-1)<2*eps) DAStudio.error('Simulink:block:invalidParameter'); end
The PostPropagationSetup method is called once all of the paramters and the output signal properties have been set and validated. Here the method is used to define three double work vectors. Work vectors are used to locally store data that is used by the rest of the code. This is equivalent to storing the discrete states of the system being modeled.
%% -------------------------------------------------------------------- %% Local Function to define the 3 Work Vectors used to store state info %% -------------------------------------------------------------------- function DoPostPropSetup(block) block.NumDworks = 3; % The first work vector stores the current state block.Dwork(1).Name = 'x0'; block.Dwork(1).Dimensions = 1; block.Dwork(1).DatatypeID = 0; % double block.Dwork(1).Complexity = 'Real'; % real block.Dwork(1).UsedAsDiscState = true; % The second work vector is used to store the next nominal sample time block.Dwork(2).Name = 'NextNomTs'; block.Dwork(2).Dimensions = 1; block.Dwork(2).DatatypeID = 0; % double block.Dwork(2).Complexity = 'Real'; % real block.Dwork(2).UsedAsDiscState = true; % The third work vector is used to store the half the nominal period block.Dwork(3).Name = 'HalfNomP'; block.Dwork(3).Dimensions = 1; block.Dwork(3).DatatypeID = 0; % double block.Dwork(3).Complexity = 'Real'; % real block.Dwork(3).UsedAsDiscState = false;
The Start method is called when all blocks within the model have been initialized but before the simulation proper starts. For this S-Function it is used to initialize the three work vectors used to store the system’s discrete states.
%% -------------------------------------------------------------------- %% Local Function to read/store state info %% -------------------------------------------------------------------- function Start(block) % Populate the Dwork vectors block.Dwork(1).Data = block.DialogPrm(3).Data; block.Dwork(2).Data = (block.DialogPrm(1).Data)/2; block.Dwork(3).Data = (block.DialogPrm(1).Data)/2;
The Outputs method is called when the block’s output signal needs to be updated. In this case it is used to output the current state (i.e. either a 1 or 0) and to determine the time of the next sample hit. Note that the Outputs method will only get called at these calculated time points.
%% -------------------------------------------------------------------- %% Local Function to define block outputs %% -------------------------------------------------------------------- function Outputs(block) % output the first state (i.e. 0 or 1) block.OutputPort(1).Data = block.Dwork(1).Data; % Calculate the time of the next sample hit, which is the next nominal time % plus a random term the size of the user specified window. block.NextTimeHit = block.Dwork(2).Data + ... 2*(rand-0.5)*block.DialogPrm(2).Data;
The Update method is called when the block’s discrete states need to be updated. This will correspond to the variable time points calculated in the Outputs method.
The code here simply toggles the state that defines the block’s output and calculates the next nominal time step (i.e. the step if there was no randomness incorporated).
%% -------------------------------------------------------------------- %% Local Function to define block discrete state updates %% -------------------------------------------------------------------- function Update(block) % toggle the first state (i.e. 0 or 1) if abs(block.Dwork(1).Data) > 2*eps % If 1 then make it 0 block.Dwork(1).Data = 0; else % If 0 then make it 1 block.Dwork(1).Data = 1; end % determine the next nominal sample time block.Dwork(2).Data = block.Dwork(2).Data + block.Dwork(3).Data;
This example has presented code for an m-code S-Function that models a square wave source signal with jitter. Other tutorials that present examples of S-Functions are available on the Writing Simulink S-Functions page and tutorials discussing Simulink and its applications for model based design are available on the Software Tutorials page.