An Introduction to the Kalman-Bucy Filter
The Kalman-Bucy Filter is a continuous time counterpart to the discrete time Kalman Filter. As with the Kalman Filter, the Kalman-Bucy Filter is designed to estimate unmeasured states of a process, usually for the purpose of controlling one or more of them.
Other tutorials discuss the Kalman Filter and its non-linear forms -- the Extended Kalman Filter and the Unscented Kalman Filter.
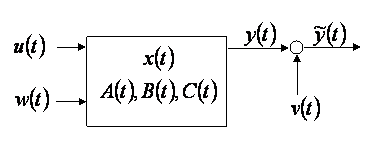
Consider the linear continuous-time process shown in Figure 1 which may be written in the following standard state-space form. (The time dependence of the parameters has been dropped to simplify the notation.)
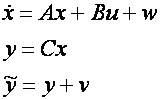
Here
- u is the vector of inputs
- x is a vector of the actual states, which may be observable but not measured.
- y is a vector of the actual process outputs.
-
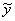is a vector of the measured process outputs. - w and v are process and output noise respectively. They are assumed to be zero mean Gaussian with covariance Q and R respectively.
Given the inputs, measured outputs and assumptions on the process and output noise, the purpose of the
Kalman-Bucy Filter is to estimate unmeasured states (assuming they are observable) and the actual
process outputs.
This is shown in Figure 2 where the estimated states are
, and 
are the estimated measured outputs.
Unlike the Kalman Filter the Kalman-Bucy filter does not use a predictor-corrector algorithm to update the state estimates. Rather it requires a differential Riccati equation to be integrated through time.
Mathematically, the filter update equations are given by
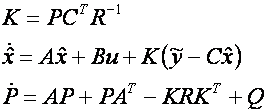
In the above equations P is an estimate of the covariance of
the measurement error and K is called the Kalman-Bucy gain.
As part of the filter implementation both
and
must be integrated through time.
Note that since P is a symmetric matrix
the number of covariance states that must be integrated may be reduced by only
considering the diagonal and terms above (or below) the diagonal.
A simple example demonstrating how to implement a Kalman-Bucy filter in Simulink can be found here.