Pricing an Asian Option in MATLAB
An Asian option is an example of an option that has a path dependent payoff. This makes it ideally suited for pricing using the Monte-Carlo approach as discussed in the Monte-Carlo Methods tutorial.
The Simulating Multiple Asset Paths in MATLAB tutorial gives an example of MATLAB code for generating the types of multiple asset paths required for option pricing using Monte-Carlo methods. That tutorial is expanded here where MATLAB code for pricing an Asian option is presented.
MATLAB Script: AsianPutCall
The following is code for generating a user specified number of simulated asset paths and then using those paths to price a standard Asian Put and Call option. The payoff of the options is given by
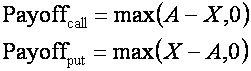
where A is the average price of the underlying asset over the life of the option and X is the strike.
% Script to price an Asian option using a monte-carlo approach. S0 =50; % Price of underlying today X = 50; % Strike at expiry mu = 0.04; % expected return sig = 0.1; % expected vol. r = 0.03; % Risk free rate dt = 1/365; % time steps etime = 50; % days to expiry T = dt*etime; % years to expiry nruns = 100000; % Number of simulated paths % Generate potential future asset paths S = AssetPaths(S0,mu,sig,dt,etime,nruns); % calculate the payoff for each path for a Put PutPayoffT = max(X-mean(S),0); % calculate the payoff for each path for a Call CallPayoffT = max(mean(S)-X,0); % discount back putPrice = mean(PutPayoffT)*exp(-r*T) callPrice = mean(CallPayoffT)*exp(-r*T)
Example Usage
The following shows the results of executing the AsianPutCall script.
putPrice =
0.3600
callPrice =
0.4932
Other MATLAB based Monte-Carlo tutorials are linked off the Software Tutorials page.