Pricing a Spread Option in MATLAB
A Spread option is an example of an option that has a payoff that is both path dependent and is dependent on multiple assets. This makes it ideally suited for pricing using the Monte-Carlo approach as discussed in the Monte-Carlo Methods tutorial.
The Simulating Multiple Asset Paths in MATLAB tutorial gives an example of a MATLAB function for generating the types of correlated multiple asset paths required for option pricing using Monte-Carlo methods. That tutorial is expanded here where MATLAB code for pricing a Spread option is presented.
MATLAB Script: Spread
The following is code for generating a user specified number of correlated asset paths for two assets and then using those paths to price a given Spread option. The payoff of the option is given by
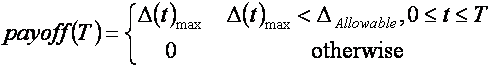
where Δ(t)max is the maximum spread between the two assets over the lifetime of the option and Δallowable is a constant pre-specified maximum allowable spread.
% Script to price a spread option using a monte-carlo approach % Some parts of this could be vectorized, but has not been done here % so that it's easier to understand what's going on. % Define required parameters S0 = [50 52]; r = 0.02; mu = [0.03 0.04]; sig = [0.1 0.15]; corr = [1 0;0 1]; allowableSpread = 4; dt = 1/365; etime = 50; % days to expiry T = dt*etime; nruns = 100000; % generate the paths S = AssetPathsCorrelated(S0,mu,sig,corr,dt,etime,nruns); % The payoff is path dependent payoff = nan*ones(nruns,1); for idx = 1:nruns maxDifference = diff(squeeze(S(:,idx,:)),1,2); maxSpread = max(abs(maxDifference)); if any(maxSpread>allowableSpread) payoff(idx) = 0; else payoff(idx) = maxSpread; end end % Determine the option price oPrice = mean(payoff)*exp(-r*T)
Example Usage
The following shows the results of executing the Spread script.
oPrice =
1.3074
Other MATLAB based Monte-Carlo tutorials are linked off the Software Tutorials page.