Option Pricing Using The Crank-Nicolson Finite Difference Method
This tutorial discusses the specifics of the Crank-Nicolson finite difference method as it is applied to option pricing. Example code implementing the Crank-Nicolson method in MATLAB and used to price a simple option is given in the Crank-Nicolson Method - A MATLAB Implementation tutorial.
The Finite Difference Methods tutorial covers general mathematical concepts behind finite diffence methods and should be read before this tutorial. Alternative finite difference methods, namely the implicit method and the explicit method, are covered in companion tutorials.
Discretizing the Black-Scholes-Merton PDE
The Crank-Nicolson finite difference method represents an average of the
implicit method and the
explicit method.
Consider the grid of points shown in Figure 1.
This represent a small portion of the general
pricing grid used in
finite difference methods.
Indices i and j represent nodes on the
pricing grid.
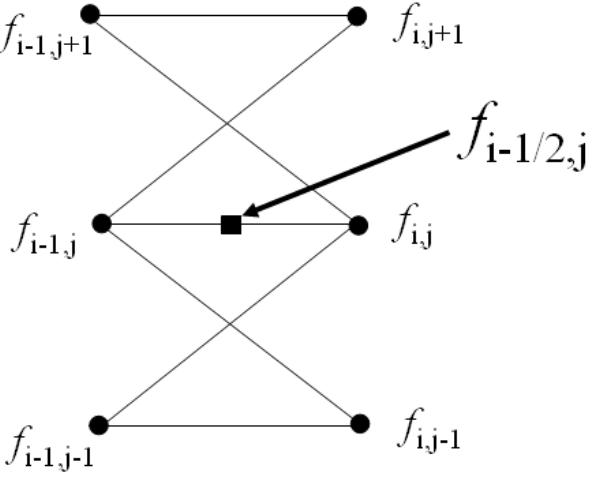
Whereas the explicit method prices the node ƒi-1, j (the central node in the left hand side) based on the values of ƒi, j+1, ƒi, j and ƒi, j-1 (the nodes on the right hand side), and the implicit method nominally prices the nodes ƒi-1, j+1, ƒi-1, j and ƒi-1, j-1 (the three nodes on the left hand side) based on the value of ƒi, j (the central node in the right hand side), the Crank-Nicolson method prices all three of the left side nodes based on the values of all three of the right side nodes. Both the implicit method and the Crank-Nicolson method achieve this by solving a set of M-1 simultaneous equations.
To derive the Crank-Nicolson difference equations consider the node ƒi-1/2, j which lies at the centre of Figure 1. (Note that a price will not be calculated for this node. Rather it is used as a mathematical convenience that will not appear in the final equations.)
The goal is to discretize the Black-Scholes-Merton partial differential equation,
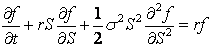
To achieve this (at node ƒi-1/2, j) the following approximations are used.
- use a central approximation
for ∂ƒ/∂t (Compare this with the
explicit method where the
backward approximation is used,
and the implicit method where the
backward approximation is used)
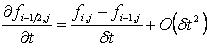
- use a central approximation for ∂ƒ/∂S
- use a standard approximation for ∂2ƒ/∂S2

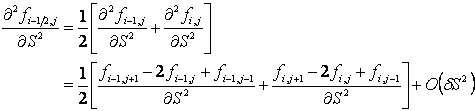
where the indices i and j represent nodes on the pricing grid.
Substituting these approximations into the Black-Scholes-Merton PDE and collecting like terms this reduces to
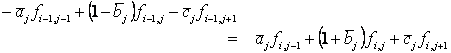
where

When Equation 1 is written for all values of i and j it leads to a set of M-1 equations in M-1 unknowns. Hence the value for ƒ at each node can be calculated uniquely by solving this set of simultaneous equations. (This can arguably be seen easier using the matrix notation shown in the following A Matrix Formulation section.)
In the option pricing framework, given the option payoff at expiry nodes then the prices Δt before expiry can be calulated, then from those prices the value 2Δt before expiry can be calculated, and working iteratively backwards through time until the option price at grid nodes for t=0 (i.e. today) can be calulated.
A Matrix Formulation
The formulation for the Crank-Nicolson method given in Equation 1
may be written in the matrix notation
![]()
where



and

This matrix notation is used in the Crank-Nicolson Method - A MATLAB Implementation tutorial.
Stability and Convergence
Two important questions to ask about any numerical algorithm are when is it stable? and if it's stable then how fast does it converge? (An iterative algorithm that is unstable will lead to the calculation of ever increasing numbers that will at some point approach infinity. On the other hand, a stable algorithm will converge to a finite solution. Typically the faster that finite solution is reached the better the algorithm.
From standard results in matrix algebra it is known that a matrix equation of the form
given in Equation 3 is stable if and only if
![]()
Equation 4 shows the infinity norm of the product of the matrices C -1D. Heuristically, if the infinity norm of C -1D is less than 1 then successive values of Fi in Equation 3 get smaller and smaller, and hence the algorithm converges, or is stable. (Alternatively if the infinity norm of C -1D is greater than 1 then successive values of Fi get larger and larger and hence diverge.)
It can be shown that the infinity norm of C -1D is less than 1 for all values of ρ, σ and δt. Hence the Crank-Nicolson finite difference method is always stable. (Compare this with the explicit method which can be unstable if δt is chosen incorrectly, and the implicit method which is also guaranteed to be stable.)
The rate of convergence of the algorithm is directly related to the truncation error introduced when approximating the partial derivatives. Hence the Crank-Nicolson method converges at the rates of Ο(δt2) and Ο(δS2). This is a faster rate of convergence than either the explicit method, or the implicit method.
A disadvantage of the Crank-Nicolson method (over the explicit method) is that it requires the inverse of a matrix (i.e. C -1) to be calculated, and the inverse of a matrix is (computationally) an expense operation to perform. Fortunately, for tri-diagonal matrices such as C (i.e. matrices that only have non-zero elements down their diagonal and the terms directly above and below their diagonal) fast inversion algorithms are available.
Another issue with the Crank-Nicolson method is that it is known to be sensitive to non-smooth boundary conditions. This is particularly the case when calculating the Greeks. A modified approach, using the explicit method for the first few time steps, then reverting to the Crank-Nicolson method for the remaining steps often overcomes this problem.
Pricing American Style Options
When pricing options that include the possibility of early exercise special care must be taken when solving Equation 3 for Fi. Taking the inverse of C to calculate a value for Fi then comparing the calculated values to the intrinsic value of the option and taking the larger value (on an element by element basis) results in incorrect option values. This is because the modified Fi will no longer satisfy Equation 3 as correct values must do.
However an iterative approach to calculating the inverse (such as the Guass-Seidel matrix inversion method) may be used successfully.